Krzysztof Gdawiec
Publikacje
Książki
 |
Domańska, D., Gdawiec, K.
Nauka programowania dla początkujących: podejście graficzne
Wydawnictwo Uniwersytetu Śląskiego, Katowice, (2017)
Streszczenie. Książka jest łagodnym wprowadzeniem w świat programowania. Jak mówi chińskie przysłowie ,,Jeden obraz wart więcej niż tysiąc słów” dlatego w książce zastosowano podejście graficzne w nauce programowania. Czytelnik nauczy się pisania programów tworzących różne graficzne obiekty i wzory w języku Processing, który jest dialektem jednego z najpopularniejszych języków programowania — języka Java. Język Processing został stworzony na MIT (Massachusetts Institute of Technology) z myślą o artystach, dlatego nauka tego języka jest bardzo prosta i szybko można w nim tworzyć różne programy graficzne. W trakcie lektury książki Czytelnik pozna różne pojęcia i techniki programowania, np. zmienne, instrukcje warunkowe, pętle, tablice, funkcje, rekurencję. Na końcu każdego z rozdziałów znajdują się zadania do samodzielnego rozwiązania. Gdyby którekolwiek z zadań okazało się zbyt trudne, na końcu książki umieszczono przykładowe rozwiązania wszystkich zadań.
Książka skierowana jest zarówno do osób, które nigdy nie miały do czynienia z programowaniem i są zainteresowane poznaniem jego podstaw, jak i do osób, które programować umieją, ale chcą odświeżyć swoją wiedzę oraz chcą się zmierzyć z, prawdopodobnie nie poznanym przez nie dotychczas, językiem Processing. Jedynymi wymaganiami jakie postawiono na starcie przed Czytelnikiem to znajomość elementów szkolnej matematyki i chęć nauczenia się programowania. |
 |
Kotarski, W., Gdawiec, K., Machnik, G.T.
Basics of Modelling and Visualization
University of Silesia, Katowice, (2009)
Abstract. This textbook presents basic concepts related to modelling and visualization tasks. Chapters 1-4 describe transformations in the plane and in the space, and geometrical forms of graphical objects such as curves, patches and fractals. Chapter 5 is about lights, materials, textures, colours that all are needed to enrich a severe appearance of pure geometrical objects leading to their photorealistic visualizations. In Chapter 6 freeware software such as POV Ray, MayaVi and Deep View are described. Using those software one can obtain photorealistic renderings and visualizations.
The textbook was prepared for students of the specialization ,,Modelling and Visualization in Bioinformatics'' but it should be helpful to anyone who is interested in computer graphics, modelling techniques, animation and visualization of data. Authors of this textbook believe that information presented in the book will be useful for students and will inspire their imagination in creation of photorealistic static 3D scenes and also will be helpful in creation of animations and visualization of data in an effective and professional way. |
Czasopisma, materiały konferencyjne
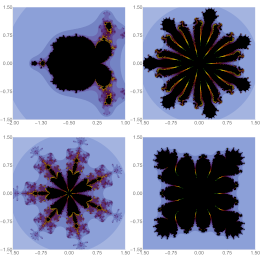 |
Roy, S., Gdawiec, K.
Numerical Algorithms (in press)
Abstract. Research on the Mandelbrot set has been ongoing for decades and occupies a significant place in the study of fractal geometry. It is obtained by employing a function in the complex plane in an iterative procedure. This method is further developed in existing literature in two ways: either by employing complicated functions of various kinds or by using iterative methods beyond the standard Picard iteration. In both cases, we use a single function to obtain the Mandelbrot set. In this paper, we propose an approach in which we use two polynomial functions instead of one. For this aim, we have utilized the Das-Debata iteration, which combines two operators into a single iterative process. Polynomials of the form z^m + p z + r, where z, p, r ∈ C, m ∈ N, and m ≥ 2, are used to derive the escape criterion. By employing the escape time algorithm, we have provided interesting graphical representations of Mandelbrot sets that exhibit notable variations in patterns compared to those obtained by the Picard iteration. To create a comparison analysis of the resulting sets based on the iteration parameters, we merged polynomials of the same degree and different degrees and changed their ordering in the iterative process. Finally, we examined two numerical measures: the average escape time and the non-escaping area index, to determine how these fractal sets rely on the iteration parameters, which turns out that the dependency of both iterative approaches is nonlinear.
|
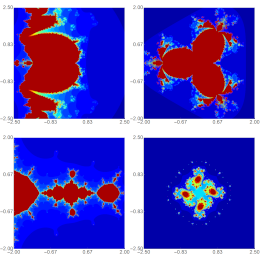 |
Nawaz, B., Gdawiec, K., Ullah, K.
The European Physical Journal Special Topics (in press)
Abstract. One of the generalizations of Mandelbrot and Julia sets introduced in the literature involves using iteration schemes from fixed-point theory to generate new classes of these sets. In this article, we propose employing the Picard-SP iteration to define a new class of Mandelbrot and Julia sets for polynomials of the form x^{k+1} + c, where x, c ∈ C and k ≥ 1. We formulate an escape criterion to generate complex graphics of the considered class of sets. Our analysis covers dynamic variations, generation timelines, shapes and colours of the resulting visuals. Furthermore, we inspect the impact of iteration parameters on Mandelbrot and Julia sets using established numerical measures from the existing literature. The results show that the sets obtained with the Picard-SP iteration are very complex, and the variation of the iteration's parameters has a significant impact on the sets. Moreover, the dependency between the parameters and the numerical measures is non-trivial and non-linear.
|
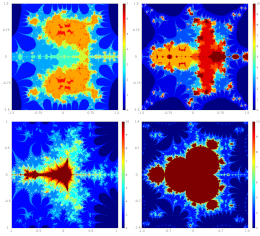 |
Antal, S., Ozgur, N., Tomar, A., Gdawiec, K.
Indian Journal of Pure and Applied Mathematics (in press)
Abstract. Recently, the generalized Fibonacci-Mann iteration scheme has been defined and used to develop an escape criterion to study mutants of the classical fractals for a function sin(z^n) + a z + c, a, c ∈ C, n ≥ 2, and z is a complex variable. In the current work, we use generalized Fibonacci-Mann iteration extended further via the notion of s-convex combination in the exploration of new mutants of celebrated Mandelbrot and Julia sets. Further, we provide a few graphical and numerical examples obtained by the use of the derived criteria.
|
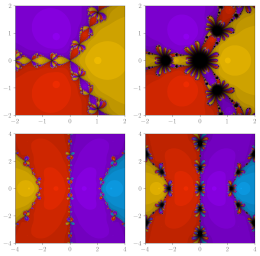 |
Naseem, A., Gdawiec, K., Qureshi, S., Argyros, I.K., Rehman, M.A., Soomro, A., Hincal, E., Hosseini, K., Padder, A.
Journal of Complexity 92, 101994, (2026)
Abstract. This study introduces an optimal fourth-order iterative method derived by combining two established methods, resulting in enhanced convergence when solving nonlinear equations. Through rigorous convergence analysis using both Taylor expansion and the Banach space framework, the fourth-order optimality condition is verified. We demonstrate the superior efficiency and stability of this new method compared to traditional alternatives. Numerical experiments confirm its effectiveness, showing a reduction in the average number of iterations and computational time. Visual analysis with polynomiographs confirms the method's robustness, focusing on convergence area index, iteration count, computational time, fractal dimension, and Wada measure of basins. These findings underscore the potential of this optimal method for tackling complex nonlinear problems in various scientific and engineering fields.
|
 |
Ouyang, P., Chung, K.W., Nicolas, A., Fathauer, R.W., Bailey, D., Gdawiec, K.
Applied Mathematics and Computation 510, 129710, (2026)
Abstract. By combining mathematical principles, modern computer graphics techniques, and the efforts of mathematically inclined artists, we present, in this paper, a visualization method for generating aesthetic patterns in hyperbolic space. To this end, we first establish fast algorithms to construct hyperbolic tilings in the Poincare disk model. Then, using templates designed by graphic artists, we specify computer techniques to render hyperbolic tilings, which results in Escher-like patterns. Moreover, we present a simple method to realize novel hyperbolic kaleidoscopic effect. To obtain more diverse patterns, we introduce several conformal mappings to create visually appealing tessellations on the other spaces. The proposed methods can be easily implemented using shaders to obtain high-quality drawings, which have good potential for application in the field of artistic decoration.
|
 |
Nawaz, B., Gdawiec, K., Ullah, K., Noorwali, M., Aphane, M.
PLoS One 20(10), e0334440, (2025)
Abstract. This manuscript investigates the convergence behavior of Suzuki's generalized nonexpansive mappings using the recently introduced Picard-Abbas iteration process. We establish both weak and strong convergence results for the associated fixed-point approximations. To demonstrate the effectiveness of our approach, a numerical example is provided. Furthermore, we generate polynomiographs based on the proposed iteration process and compare them with those produced by existing methods, highlighting the advantages and visual insights offered by our scheme.
|
 |
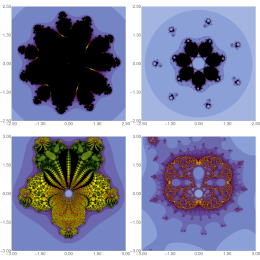
Gdawiec, K., dos Santos, Y.G.S., Fariello, R.
Chaos 35(10), 103114, (2025)
Abstract. In recent years, significant research has been conducted on using various iteration schemes derived from fixed-point theory to generate Mandelbrot and Julia sets in the complex space. Building on these advancements, this work explores the application of the Garodia-Uddin iteration scheme to construct Julia sets of q → q^k + c in the quaternion space. Specifically, we establish the escape criterion for the Garodia-Uddin orbit and analyse the symmetry of the Julia set for the even values of k. Additionally, we provide and discuss 2D and 3D graphical examples of sets generated from the Garodia-Uddin iteration scheme. Furthermore, we investigate the effect of a key parameter in the proposed approach on the average escape time, non-escaping area index, and fractal dimension for 2D cross-sections of quaternion Julia sets of varying degrees. Finally, the Julia sets obtained are compared to the ones which come from the Picard-Mann iteration scheme.
|
 |
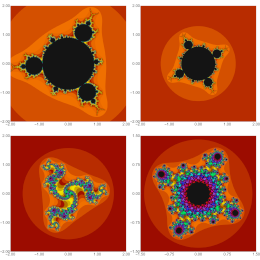
Roy, S., Gdawiec, K., Saha, P., Choudhury, B.S.
Chaos, Solitons & Fractals 199, part 1, 116617, (2025)
Abstract. Mandelbrot sets, and Julia sets are two key concepts in fractal geometry. A useful tool to generate these fractal sets is the escape time algorithm, which is an iterative scheme based on a complex function paired with some well-known fixed point iteration methods. The existing literature primarily generates Mandelbrot and Julia sets through the use of a complex polynomial or a complex rational function. This work presents a novel technique in light of this fractal generation process. We employ an iterative method that involves two operators, which was introduced to identify common fixed points, i.e., the Das-Debata iteration. The escape criterion for the Das-Debata iteration is derived by utilizing a complex polynomial and rational function and by altering the positions of the functions in the iteration process. Some illustrative examples of Mandelbrot and Julia sets obtained through the proposed iterative method are provided. We compare the generated fractals by the two orders of the functions in the iterative method. To determine the dependence of fractal sets on the iteration parameters, we analyze two numerical measures: the average escape time and the non-escaping area index. In the two considered orders of the functions, it is revealed that their dependence is nonlinear.
|
 |
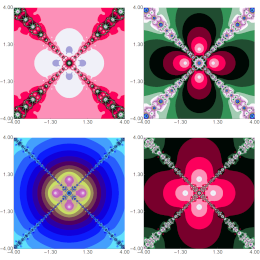
Gdawiec, K., Tanveer, M.
Axioms 14(6), 404, (2025)
Abstract. In this paper, we introduce a generalised formulation of the logistic map extended to the complex plane and correspondingly redefine the classical Mandelbrot and Julia sets within this broader framework. Central to our approach is the development of an escape criterion based on the Picard orbit, which underpins the escape-time algorithms employed for graphical approximations of these sets. We analyse the structural and dynamical properties of the resulting Mandelbrot and Julia sets, emphasising their inherent symmetries through detailed visualisations. Furthermore, we examine how variations in a key parameter of the generalised map affect two critical numerical metrics: the average escape time and the non-escaping area index. Our computational study reveals that, particularly for Julia sets, these dependencies are characterised by intricate, highly non-linear behaviour - highlighting the profound complexity and sensitivity of the system under this generalised mapping.
|
 |
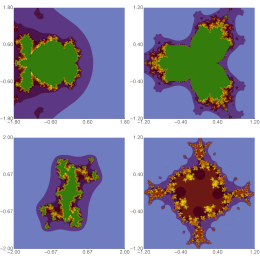
Nawaz, B., Gdawiec, K., Ullah, K.
Journal of Computational and Applied Mathematics 469, 116649, (2025)
Abstract. In this paper, we investigate the convergence properties of mappings that satisfy condition (E) by employing the recently introduced Picard-Abbas iteration process. We establish both weak and strong fixed-point convergence results for these mappings. To validate our findings, we provide a novel numerical example. Furthermore, we generate polynomiographs using the proposed iteration process and compare them with those obtained from other methods. This comparison highlights the effectiveness and potential advantages of our approach.
|
 |
Nawaz, B., Gdawiec, K., Ullah, K., Aphane, M.
PLoS One 20(3), e0315271, (2025)
Abstract. Nowadays, many researchers are employing various iterative techniques to analyse the dynamics of fractal patterns. In this paper, we explore the formation of Mandelbrot and Julia sets using the Picard-Thakur iteration process, extended with s-convexity. To achieve this, we establish an escape criterion using a complex polynomial of the form x^{k+1} + c, where k ≥ 1 and x, c ∈ C. Based on our proposed algorithms, we provide graphical illustrations of the Mandelbrot and Julia sets. Additionally, we extend our research to examine the relationship between the sizes of Mandelbrot and Julia sets and the iteration parameters, utilising some well-known methods from the literature.
|
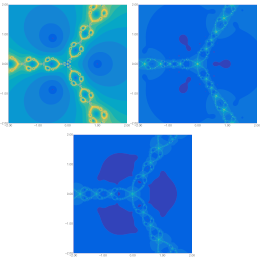 |
Nawaz, B., Ullah, K., Gdawiec, K.
Numerical Algorithms 98(4), 1943-1964, (2025)
Abstract. In this manuscript, we introduce a novel hybrid iteration process called the Picard-SP iteration process. We apply this new iteration process to approximate fixed points of generalized alpha-nonexpansive mappings. Convergence analysis of our newly proposed iteration process is discussed in the setting of uniformly convex Banach spaces and results are correlated with some other existing iteration processes. The dominance of the newly proposed iteration process is exhibited with the help of a new numerical example. In the end, the comparison of polynomiographs generated by other well-known iteration processes with our proposed iteration process has been presented to make a strong impression of our proposed iteration process.
|
 |
Nawaz, B., Ullah, K., Gdawiec, K.
Soft Computing 29(2), 435-455, (2025)
Abstract. This paper proposes a novel hybrid iteration process, namely the Picard-CR iteration process. We apply the proposed iteration process for the numerical reckoning of fixed points of generalized alpha-nonexpansive mappings. We establish weak and strong convergence results of generalized alpha-nonexpansive mappings. This study demonstrates the superiority of the hybrid approach in terms of convergence speed. Moreover, we numerically compare the proposed iteration process with other well-known ones from the literature. In the comparison, we consider two problems: finding a fixed point of a generalized alpha-nonexpansive mapping and finding roots of a complex polynomial. In the second problem, we use the so-called polynomiography in the analysis. The results showed that the proposed iteration scheme is better than other three-parameter iteration schemes from the literature. Using the proven fixed-point results, we also obtain solutions to fractional differential equations.
|
 |
Qureshi, S., Soomro, A., Argyros, I.K., Gdawiec, K., Akgul, A., Alquran, M.
Communications in Nonlinear Science and Numerical Simulation 143, 108631, (2025)
Abstract. There are many different fields of study where nonlinear polynomial-based models arise and need to be solved, making the study of root-finding iterative solvers an important topic of research. Our goal was to use the two most significant fractional differential operators, Caputo and Riemann-Liouville, and an existing time-efficient three-step Newton-like iterative solver to address the growing interest in fractional calculus. The classical solver is preserved alongside a damping term created within it that tends to 1 as the fractional order alpha approaches 1. The solvers' local and semi-local convergence are investigated, and the stability trade-off with convergence speed is discussed at length. The suggested fractional-order solvers are tested on a number of nonlinear one-dimensional polynomial-based problems that come up in image processing, mechanical design, and civil engineering, such as beam deflection; and many more.
|
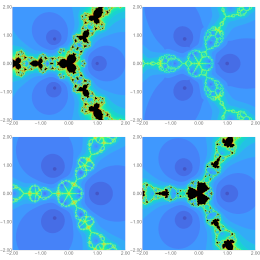 |
Naseem, A., Argyros, I.K., Qureshi, S., Rehman, M.A., Soomro, A., Gdawiec, K., Abdulganiy, R.I.
Acta Applicandae Mathematicae 195(1), 1, (2025)
Abstract. Algorithms that locate roots are used to analyze nonlinear equations in computer science, mathematics, and physical sciences. In order to speed up convergence and increase computational efficiency, memory-based root-seeking algorithms may look for the previous iterations. Three memory-based methods with a convergence order of about 2.4142 and one method without memory with third-order convergence are devised using both Taylor's expansion and the backward difference operator. We provide an extensive analysis of local and semilocal convergence. We also use polynomiography to analyze the methods visually. Finally, the proposed iterative approaches outperform a number of existing memory-based methods when applied to one-dimensional nonlinear models taken from different fields of science and engineering.
|
 |
Ouyang, P., Chung, K.W., Fathauer, R.W., Nicolas, A., Pang, J.-H., Cao, S.-Y., Gdawiec, K.
Journal of Computer Science and Technology 39(6), 1466-1479, (2024)
Abstract. "Smaller and Smaller" is a woodcut by the Dutch artist M.C. Escher in which the lizards designed in a rosette tiling approach the centre by geometric series. This paper proposes an easy method to generate drawings similar to "Smaller and Smaller". To this end, the geometrical structure of rosette tilings is first considered from the viewpoint of the symmetry group in detail. This gives a simple way to construct rosette tilings. Then, a one-to-one mapping between kite-shaped and square regions is presented to embed a pre-designed template into kite-shaped tiles of rosette tilings. Next, the algorithms for rendering the rosette tilings are discussed. Finally, some detailed implements of producing rosette drawings are specified. The presented examples show that by using the existing rich wallpaper templates, the method proposed in the paper can generate a variety of Escher-like rosette drawings.
|
 |
Almutairi, D.K., Argyros, I.K., Gdawiec, K., Qureshi, S., Soomro, A., Jamali, K.H., Alquran, M., Tassaddiq, A.
AIMS Mathematics 9(11), 32014-32044, (2024)
Abstract. Many researchers have proposed iterative algorithms for nonlinear equations and systems of nonlinear equations; similarly, in this paper, we developed two two-step algorithms of the predictor--corrector type. A combination of Taylor's series and the composition approach is used. One of the algorithms has an eighth order of convergence and a high-efficiency index of approximately 1.5157, which is higher than that of some existing algorithms, while the other possesses fourth-order convergence. The convergence analysis is carried out in both senses, that is, local and semi-local convergence. Various complex polynomials of different degrees are considered for visual analysis via the basins of attraction. We analyze and compare the proposed algorithms with other existing algorithms having same features. The visual results show that the modified algorithms have a higher convergence rate compared to existing algorithms. Real-life systems related to chemistry, astronomy, and neurology are used in the numerical simulations. The numerical simulations of the test problems reveal that the proposed algorithms surpass similar existing algorithms established in the literature.
|
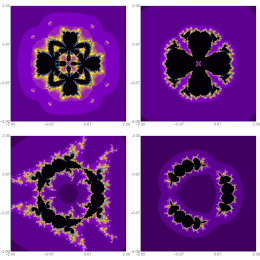 |
Tanveer, M., Gdawiec, K.
Qualitative Theory of Dynamical Systems 23(1 supplement), 297, (2024)
Abstract. Mandelbrot set is one of the most fascinating objects in mathematics, so in the literature, one can find many studies related to this set. Moreover, there are many different extensions and generalizations of the classical Mandelbrot set. The two most popular extensions are the use of various kinds of functions and iterations. In this paper, firstly, we replace the constant c in the classical z^p + c function used in the definition of Mandelbrot set with log c^t, where t ∈ R and t ≥ 1. Secondly, we replace the Picard iteration with the CR iteration scheme. For this combination of function and iteration, we prove the escape criterion for the escape-time algorithm used to generate some images of the proposed sets. Moreover, we study the dependency between the iteration's parameters and two numerical measures (average number of iterations and generation time). We show that this dependency is complex and non-linear.
|
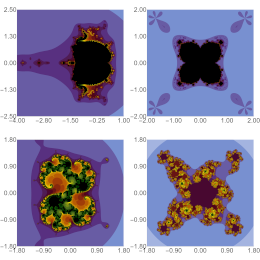 |
Nawaz, B., Ullah, K., Gdawiec, K.
Chaos, Solitons & Fractals 188, 115516, (2024)
Abstract. In this manuscript, we introduce the M-iteration process for generating Mandelbrot and Julia sets. We establish an escape criterion for a polynomial of the form x^{k+1} + c in the complex plane corresponding to the M-iteration process. Next, we present some graphical examples of Mandelbrot and Julia sets generated using the proven escape criterion and the escape-time algorithm. We also compare the images generated with the M, Mann, and Picard-Mann iterations. Moreover, we study the dependency between the iterations' parameters and three numerical measures (the average escape time, non-escaping area index, and box-counting dimension) used in the literature. The results show that fractal images generated using the M-iteration are entirely different from those generated using the other two analysed iteration schemes. Moreover, the dependencies are highly non-linear and vary between the iterations.
|
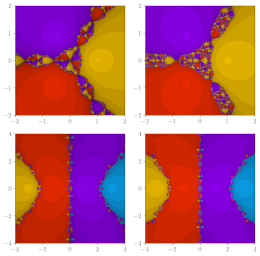 |
Qureshi, S., Argyros, I.K., Jafari, H., Soomro, A., Gdawiec, K.
MethodsX 13, 102865, (2024)
Abstract. This study introduces a family of root-solvers for systems of nonlinear equations, leveraging the Daftardar--Gejji and Jafari Decomposition Technique coupled with the midpoint quadrature rule. Despite the existing application of these root solvers to single-variable equations, their extension to systems of nonlinear equations marks a pioneering advancement. Through meticulous derivation, this work not only expands the utility of these root solvers but also presents a comprehensive analysis of their stability and semilocal convergence; two areas of study missing in the existing literature. The convergence of the proposed solvers is rigorously established using Taylor series expansions and the Banach Fixed Point Theorem, providing a solid theoretical foundation for semilocal convergence guarantees. Additionally, a detailed stability analysis further underscores the robustness of these solvers in various computational scenarios. The practical efficacy and applicability of the developed methods are demonstrated through the resolution of five real-world application problems, underscoring their potential in addressing complex nonlinear systems. This research fills a significant gap in the literature by offering a thorough investigation into the stability and convergence of these root solvers when applied to nonlinear systems, setting the stage for further explorations and applications in the field.
|
 |
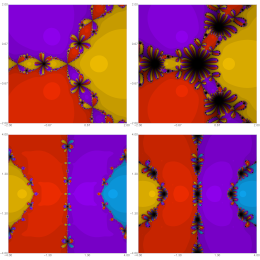
Qureshi, S., Soomro, A., Naseem, A., Gdawiec, K., Argyros, I.K., Alshaery, A.A., Secer, A.
Mathematical Methods in the Applied Sciences 47(7), 5509-5531, (2024)
Abstract. Root-finding methods solve equations and identify unknowns in physics, engineering, and computer science. Memory-based root-seeking algorithms may look back to expedite convergence and enhance computational efficiency. Real-time systems, complicated simulations, and high-performance computing demand frequent, large-scale calculations. This article proposes two unique root-finding methods that increase the convergence order of the classical Newton-Raphson approach without increasing evaluation time. Taylor's expansion uses the classical Halley method to create two memory-based methods with an order of 2.4142 and an efficiency index of 1.5538. We designed a two-step memory-based method with the help of Secant and Newton-Raphson (NR) algorithms using a backward difference quotient. We demonstrate memory-based approaches' robustness and stability using visual analysis via polynomiography. Local and semilocal convergence are thoroughly examined. Finally, proposed memory-based approaches outperform several existing memory-based methods when applied to models including a thermistor, path traversed by an electron, sheet-pile wall, adiabatic flame temperature, and blood rheology nonlinear equation.
|
 |
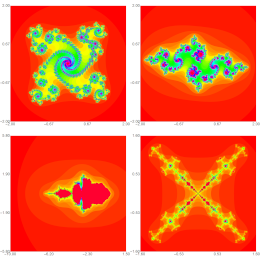
Argyros, I.K., Gdawiec, K., Qureshi, S., Soomro, A., Hincal, E., Regmi, S.
Applied Numerical Mathematics 201, 446-464, (2024)
Abstract. The examination of nonlinear equations is essential in diverse domains such as science, business, and engineering because of the widespread occurrence of nonlinear phenomena. The primary obstacle in computational science is to create numerical algorithms that are both computationally efficient and possess a high convergence rate. This work tackles these problems by presenting a three-step nonlinear, time-efficient numerical method for solving nonlinear models. The selected method exhibits a convergence of sixth order and an efficiency index of 1.4310, with the added benefit of only requiring five function evaluations per iteration. This study diverges from earlier research by emphasizing the use of first-order derivatives instead of higher-order derivatives. As a result, the method becomes more versatile and applicable. It is possible to estimate solutions that are locally different in Banach spaces by looking at convergence on both local and semi-local levels. The stability and performance of the scheme are also checked by using polynomiography to do a visual analysis and compare it to other schemes in terms of convergence, speed, and CPU time.
|
 |
Kumari, S., Gdawiec, K., Nandal, A., Kumar, N., Chugh, R.
Numerical Algorithms 96(1), 211-236, (2024)
Abstract. In this paper, we visualize and analyse the dynamics of fractals (Julia and Mandelbrot sets) for complex polynomials of the form T(z) = z^n + m z + r, where n ≥ 2 and m, r ∈ C, by adopting the viscosity approximation type iteration process which is most widely used iterative method for finding fixed points of non-linear operators. We establish a convergence condition in the form of escape criterion which allows to adapt the escape-time algorithm to the considered iteration scheme. We also present some graphical examples of the Mandelbrot and Julia fractals showing the dependency of Julia and Mandelbrot sets on complex polynomials, contraction mappings and iteration parameters. Moreover, we propose two numerical measures that allow the study of the dependency of the set shape change on the values of the iteration parameters. Using these two measures, we show that the dependency for the considered iteration method is non-linear.
|
 |
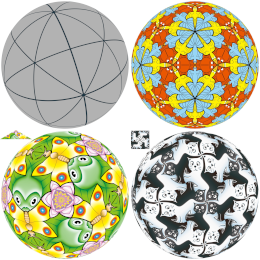
Qureshi, S., Argyros, I.K., Soomro, A., Gdawiec, K., Shaikh, A.A., Hincal, E.
Numerical Algorithms 95(4), 1715-1745, (2024)
Abstract. In this work, a new optimal iterative algorithm is presented with fourth-order accuracy for root-finding of real functions. It uses only function as well as derivative evaluation. The algorithm is obtained as a combination of existing third-order methods by specifying a parameter involved. The algorithm is based on local and semilocal analysis and has been specifically designed to improve efficiency and accuracy. The proposed algorithm represents a significant improvement over existing iterative algorithms. In particular, it is tested on a range of polynomial functions and was found to produce accurate and efficient results, with improved performance over existing algorithms in terms of both speed and accuracy. The results demonstrate the effectiveness of the proposed algorithm and suggest that it has great potential for use in a wide range of applications in polynomiography and other areas of mathematical analysis.
|
 |
Gdawiec, K., Chung, K.W., Nicolas, A., Bailey, D., Ouyang, P.
Computer Graphics Forum 43(1), e14999, (2024)
Abstract. In this paper, we present a method for creating Escher-like spherical patterns with regular polyhedron symmetries. Using the generators of the symmetry groups associated with regular polyhedra, we first provide fast algorithms to construct spherical tilings. Then, to obtain Escher-like patterns, we specify texturing techniques to decorate the resulting tilings. Moreover, we present a strategy to create a novel dynamic effect of Escher-like kaleidoscopes in which the motifs have a complete body. The method has the advantages of simple implementation, fast calculation, good graphics, and artistic effects, which can be used to create rich elegant spherical patterns.
|
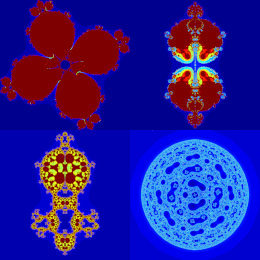 |
Rawat, S., Prajapati, D.J., Tomar, A., Gdawiec, K.
Mathematics and Computers in Simulation 220, 148-169, (2024)
Abstract. In this paper, we introduce a generalized rational map to develop a theory of escape criterion via the SP-iteration process equipped with s-convexity. Furthermore, we develop algorithms for the exploration of unique kinds of Mandelbrot as well as Julia sets. We demonstrate graphically the change in colour, size, and shape of images with the change in values of the considered iteration's parameters. The new fractals thus obtained are visually very pleasing and attractive. Most of these newly generated fractals resemble natural objects around us. Moreover, we numerically study the dependence between the iteration's parameters and the set size. The experiments show that this dependency is non-linear. We believe that the obtained conclusions will motivate researchers who are interested in fractal geometry.
|
 |
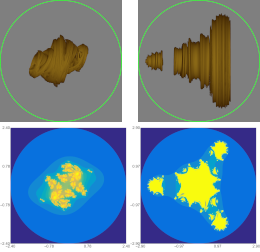
Gdawiec, K., Argyros, I.K., Qureshi, S., Soomro, A.
Journal of Computational Science 74, 102166, (2023)
Abstract. To avoid divergence in the traditional iterative root-finding methods the homotopy continuation approach is commonly used in the literature. However, neither their theoretical analysis in terms of local and semilocal convergence nor their stability is explored in the present literature. In this paper, we describe the homotopy continuation (HC) version of a fourth-order accurate optimal iterative algorithm. The local and semilocal convergence of the HC-based algorithm, including the basins of attraction, are being examined for the first time in the literature. These basins are used to demonstrate that the HC variant is more stable than the traditional iterative approach, which is widely held to be advantageous. The usual iterative method with first-order derivative is shown to be replaceable by its equivalent HC counterpart to achieve better stability for several numerical problems selected from academia and industry.
|
 |
Gdawiec, K., Fariello, R., dos Santos, Y.G.S.
Nonlinear Dynamics 111(18), 17591-17603, (2023)
Abstract. In recent years, an extensive study on the use of various iteration schemes from fixed point theory for the generation of Mandelbrot and Julia sets in complex space has been carried out. In this work, inspired by these progresses, we study the use of the Picard-Mann iteration scheme for the Julia sets in the quaternion space. Specifically, in our study, we prove the escape criterion of the Picard-Mann orbit and examine the symmetry of the Julia set for the quadratic function. Moreover, we present and discuss some 2D and 3D graphical examples of the sets generated using the Picard-Mann iteration scheme. We further analyse the influence of a parameter of interest used in the Picard-Mann iteration scheme on the average number of iterations for 2D cross sections of quaternion Julia sets of different degrees.
|
 |
Chung, K.W., Ouyang, P., Nicolas, A., Cao, S., Bailey, D., Gdawiec, K.
Mathematical Methods in the Applied Sciences 46(13), 14489-14508, (2023)
Abstract. Dutch graphic artist M.C. Escher created many famous drawings with a deep mathematical background based on wallpaper symmetry, hyperbolic geometry, spirals, and regular polyhedra. However, he did not attempt any spiral drawings in hyperbolic space. In this paper, we consider a modified hyperbolic geometry by removing the condition that a geodesic is orthogonal to the unit circle in the Poincare model. We show that spiral symmetry and the similarity property exist in this modified geometry so that the creation of uncommon hyperbolic spiral drawings is possible. To this end, we first establish the theoretical foundation for the proposed method by deriving a contraction mapping and a rotation for constructing modified hyperbolic spiral tilings (MHSTs) and introduce symmetry groups to analyse the structure of MHSTs. Then, to embed a pre-designed wallpaper template into the tiles, we derive a one-to-one mapping between a tile of MHST and a rectangle. Finally, we specify some technical implementation details and give a gallery of the resulting MHST drawings. Using existing wallpaper templates, the proposed method is able to generate a great variety of exotic Escher-like drawings.
|
 |
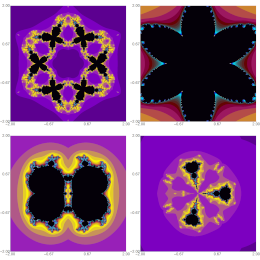
Kumari, S., Gdawiec, K., Nandal, A., Kumar, N., Chugh, R.
Aequationes Mathematicae 97(2), 257-278, (2023)
Abstract. In this paper, we present an application of the viscosity approximation type iterative method introduced by Nandal et al. (Iteration Process for Fixed Point Problems and Zeros of Maximal Monotone Operators, Symmetry, 2019) to visualize and analyse the Julia and Mandelbrot sets for a complex polynomial of the type T(z) = z^n + p z + r, where p, r ∈ C, and n ≥ 2. This iterative method has many applications in solving various fixed point problems. We derive an escape criterion to visualize Julia and Mandelbrot sets via the proposed viscosity approximation type method. Moreover, we present several graphical examples of the fractals generated with the proposed iteration method.
|
 |
Tanveer, M., Nazeer, W., Gdawiec, K.
Mathematics and Computers in Simulation 209, 184-204, (2023)
Abstract. Since its introduction, the Mandelbrot set has been studied and generalised in various directions. Some authors generalized it by using iterations from fixed point theory, whereas others characterized it by using different complex functions or polynomials. In this paper, we replace the constant c in the classical z^p + c function with log c^t, where t ∈ R and t ≥ 1. Moreover, we prove escape criteria for the Mann and Picard-Mann iterations in which we use the modified function. Then, we present graphical and numerical examples showing the behaviour of the generated sets depending on the parameters of the iterations and the parameter t. Using the proposed approach, we can generate a great variety of fascinating fractal patterns, and when t ∈ N the sets form rosette patterns.
|
 |
Ouyang, P., Gdawiec, K., Nicolas, A., Bailey, D.R.M., Chung, K.W.
ACM Transactions on Graphics 42(2), Article no. 18, (2023)
Abstract. Whirlpools, by the Dutch graphic artist M.C. Escher, is a woodcut print in which fish interlock as a double spiral tessellation. Inspired by this print, in this paper we extend the idea and present a general method to create Escher-like interlocking spiral drawings of N whirlpools. To this end, we first introduce an algorithm for constructing regular spiral tiling T. Then, we design a suitable spiral tiling T and use N copies of T to compose an interlocking spiral tiling K of N whirlpools. To create Escher-like drawings similar to the print, we next specify realization details of using wallpaper templates to decorate K. To enhance the aesthetic appeal, we propose several measures to minimize motif overlaps of the spiral drawings. Technologically, we develop algorithms for generating Escher-like drawings that can be implemented using shaders. The method established is thus able to generate a great variety of exotic Escher-like interlocking spiral drawings.
|
 |
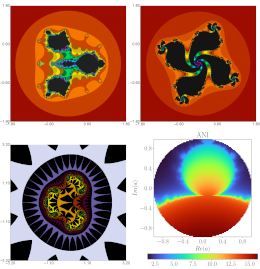
Ouyang, P., Chung, K.W., Bailey, D., Nicolas, A., Gdawiec, K.
The Visual Computer 38(11), 3923-3935, (2022)
Abstract. In this paper, using both hand-drawn and computer-drawn graphics, we establish a method to generate advanced Escher-like spiral tessellations. We first give a way to achieve simple spiral tilings of cyclic symmetry. Then, we introduce several conformal mappings to generate three derived spiral tilings. To obtain Escher-like tessellations on the generated tilings, given pre-designed wallpaper motifs, we specify the tessellations' implementation details. Finally, we exhibit a rich gallery of the generated Escher-like tessellations. According to the proposed method, one can produce a great variety of exotic Escher-like tessellations that have both good aesthetic value and commercial potential.
|
 |
Kumari, S., Gdawiec, K., Nandal, A., Postolache, M., Chugh, R.
Chaos, Solitons & Fractals 163, 112540, (2022)
Abstract. Iterative procedures have been proved as a milestone in the generation of fractals. This paper presents a new approach to visualize Mandelbrot and Julia sets for complex polynomials of the form W(z) = z^n + mz + r; n ≥ 2 where m, r ∈ C, and biomorphs for any complex function through a viscosity approximation method which is among the most widely used iterative methods for finding fixed points of non-linear operators. We derive novel escape criterion for generating Julia and Mandelbrot sets via proposed viscosity approximation method. Moreover, we visualize the sets using the escape time algorithm and the proposed iteration. Then, we discuss the shape change of the obtained sets depending on the parameters of the iteration using graphical and numerical experiments. The presented examples reveal that this change can be very complex, and we are able to obtain a great variety of shapes.
|
 |
Gdawiec, K., Lisowska, A., Kotarski, W.
Lecture Notes in Computer Science, vol. 13351, pp. 162-168, (2022)
Abstract. Recently, the pseudo-Newton method was proposed to solve the problem of finding the points for which the maximal modulus of a given polynomial over the unit disk is attained. In this paper, we propose a modification of this pseudo-Newton method, which relies on the use of fractional order derivatives (Caputo and Riemann-Liouville derivatives) instead of the classical one. The proposed modification is evaluated twofold: visually via polynomiographs coloured according to the number of needed iterations, and numerically by using the convergence area index, the average number of iterations and generation time of polynomiographs. The experimental results show that the fractional pseudo-Newton method for some fractional orders behaves better in comparison to the standard pseudo-Newton algorithm, which means a decrease in the number of iterations and the higher convergence index over the standard algorithm.
|
 |
Gościniak, I., Gdawiec, K.
Lecture Notes in Computer Science, vol. 13350, pp. 623-636, (2022)
Abstract. The root-finding problem is very important in many applications and has become an extensive research field. One of the directions in this field is the use of various iteration schemes. In this paper, we propose a new generalised iteration scheme. The schemes like Mann, Ishikawa, Das-Debata schemes are special cases of the proposed iteration. Moreover, we use the proposed iteration with the PSO-based Newton-like method in two tasks. In the first task, we search for the roots, whereas in the second one for patterns with aesthetic features. The obtained results show that the proposed iteration can decrease the average number of iterations needed to find the roots and that we can generate patterns with potential artistic applications.
|
 |
Gdawiec, K., Adewinbi, H.
Applied Sciences 12(6), 2923, (2022)
Abstract. In the literature, we can find various methods for generating artistic patterns. One of the methods is the orbit trap method. In this paper, we propose various modifications of a variant of the orbit trap method that generates patterns with wallpaper symmetry. The first modification relies on replacing the Picard iteration (used in the original method) with the S-iteration known from the fixed point theory. Moreover, we extend the parameters in the S-iteration from scalar to vector ones. In the second modification, we replace the Euclidean metric used in the orbit traps with other metrics. Finally, we propose three new orbit traps. The presented examples show that using the proposed method, we are able to obtain a great variety of interesting patterns. Moreover, we show that a proper selection of the orbit traps and the mapping used by the method can lead to patterns that possess a local fractal structure.
|
Gościniak, I., Gdawiec, K., Woźniak, K., Machoy, M.
Procedia Computer Science 192, 1856-1865, (2021)
Abstract. Applications of the fractal dimension include the analysis and interpretation of medical images. The article presents a method for determining image features that are based on fractal dimension. In the proposed method, an optimization process (modified semimultifractal optimization algorithm) creates a division into sub-areas similarly to a multi-resolution method. Using this division, a characteristic spectrum based on the fractal dimensions is calculated. This spectrum is applied to the recognition method of X-ray images of teeth. The obtained experimental results showed that the proposed method can effectively recognize such images.
|
|
 |
Shahid, A.A., Nazeer, W., Gdawiec, K.
Monatshefte für Mathematik 195(4), 565-584, (2021)
Abstract. In recent years, researchers have studied the use of different iteration processes from fixed point theory in the generation of complex fractals. For instance, the Mann, Ishikawa, Noor, Jungck-Mann and Jungck-Ishikawa iterations have been used. In this paper, we study the use of the Picard-Mann iteration with s-convexity in the generation of Mandelbrot and Julia sets. We prove the escape criterion for the (k+1)st degree complex polynomial. Moreover, we present some graphical and numerical examples regarding Mandelbrot and Julia sets generated using the proposed iteration.
|
 |
Ouyang, P., Chung, K.W., Nicolas, A., Gdawiec, K.
ACM Transactions on Graphics 40(3), Article no. 31, (2021)
Abstract. A fractal tiling (f-tiling) is a kind of rarely explored tiling by similar polygonal tiles which possesses self-similarity and the boundary of which is a fractal. Based on a tiling by similar isosceles right triangles, Dutch graphic artist M.C. Escher created an ingenious print Square Limit in which fish are uniformly reduced in size as they approach the boundaries of the tiling. In this paper, we present four families of f-tilings and propose an easy-to-implement method to achieve similar Escher-like drawings. By systematically investigating the local star-shaped structure of f-tilings, we first enumerate four families of f-tilings admitted by kite-shaped or dart-shaped prototiles. Then, we establish a fast binning algorithm for visualizing f-tilings. To facilitate the creation of Escher-like drawings on the reported f-tilings, we next introduce one-to-one mappings between the square, and kite and dart, respectively. This treatment allows a pre-designed square template to be deformed into all prototiles considered in the paper. Finally, we specify some technical implementations and present a gallery of the resulting Escher-like drawings. The method established in this paper is thus able to generate a great variety of exotic Escher-like drawings.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Lecture Notes in Computer Science, vol. 12742, pp. 330-337, (2021)
Abstract. In this paper, we propose an improvement of the Robust Newton's Method (RNM). The RNM is a generalisation of the known Newton's root finding method restricted to polynomials. Unfortunately, the RNM is slow. Thus, in this paper, we propose the acceleration of this method by replacing the standard Picard iteration in the RNM by the S-iteration. This leads to an essential acceleration of the modified method. We present the advantages of the proposed algorithm over the RNM using polynomiagraphs and some numerical measures. Moreover, we present its possible application to the generation of artistic patterns.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Nonlinear Dynamics 104(1), 297-331, (2021)
Abstract. There are two main aims of this paper. The first one is to show some improvement of the Robust Newton's Method (RNM) introduced recently by Kalantari. The RNM is a generalisation of the well-known Newton's root finding method. Since the base method is undefined at critical points, the RNM allows working also at such points. In this paper, we improve the RNM method by applying the Mann iteration instead of the standard Picard iteration. This leads to an essential decrease in the number of root finding steps without visible destroying the sharp boundaries among the basins of attractions presented in polynomiographs. Furthermore, we investigate visually the dynamics of the RNM with the Mann iteration together with the basins of attraction for varying Mann's iteration parameter with the help of polynomiographs for several polynomials. The second aim of this paper is to present the intriguing polynomiographs obtained from the dynamics of the RNM with the Mann iteration under various sequences used in this iteration. The obtained polynomiographs differ considerably from the ones obtained with the RNM and are interesting from the artistic perspective. Moreover, they can easily find applications in wallpaper or fabric design.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Numerical Algorithms 86(3), 953-1010, (2021)
Abstract. The aim of this paper is to visually investigate the dynamics and stability of the process in which the classic derivative is replaced by the fractional Riemann-Liouville or Caputo derivatives in the standard Newton root-finding method. Additionally, instead of the standard Picard iteration, the Mann, Khan, Ishikawa and S iterations are used. This process when applied to polynomials on complex plane produces images showing basins of attractions for polynomial zeros or images representing the number of iterations required to achieve any polynomial root. The images are called as polynomiographs. In this paper, we use the colouring according to the number of iterations which reveals the speed of convergence and dynamic properties of processes visualised by polynomiographs. Moreover, to investigate the stability of the methods we use basins of attraction. To compare numerically the modified root-finding methods among them we demonstrate their action for polynomial z^3 - 1 on complex plane.
|
 |
Tanveer, M., Nazeer, W., Gdawiec, K.
Indian Journal of Pure and Applied Mathematics 51(4), 1285-1303, (2020)
Abstract. In recent years, researchers have studied the use of different iteration processes from fixed point theory for the generation of complex fractals. Examples are the Mann, the Ishikawa, the Noor, the Jungck-Mann and the Jungck-Ishikawa iterations. In this paper, we present a generalisation of complex fractals, namely Mandelbrot, Julia and multicorn sets, using the Jungck-CR implicit iteration scheme. This type of iteration does not reduce to any of the other iterations previously used in the study of complex fractals; thus, this generalisation gives rise to new fractal forms. We prove a new escape criterion for a polynomial of the following form z^m - a z + c, where a, c ∈ C, and present some graphical examples of the obtained complex fractals.
|
 |
Gościniak, I., Gdawiec, K.
Soft Computing 24(18), 14135-14155, (2020)
Abstract. Many algorithms that iteratively find solution of an equation require tuning. Due to the complex dependence of many algorithm’s elements, it is difficult to know their impact on the work of the algorithm. The article presents a simple root-finding algorithm with self-adaptation that requires tuning, similarly to evolutionary algorithms. Moreover, the use of various iteration processes instead of the standard Picard iteration is presented. In the algorithm’s analysis, visualizations of the dynamics were used. The conducted experiments and the discussion regarding their results allow to understand the influence of tuning on the proposed algorithm. The understanding of the tuning mechanisms can be helpful in using other evolutionary algorithms. Moreover, the presented visualizations show intriguing patterns of potential artistic applications.
|
 |
Gościniak, I., Gdawiec, K.
Entropy 22(7), 734, (2020)
Abstract. There is a huge group of algorithms described in the literature that iteratively find solutions of a given equation. Most of them require tuning. The article presents root-finding algorithms that are based on the Newton-Raphson method which iteratively finds the solutions, and require tuning. The modification of the algorithm implements the best position of particle similarly to the particle swarm optimisation algorithms. The proposed approach allows visualising the impact of the algorithm's elements on the complex behaviour of the algorithm. Moreover, instead of the standard Picard iteration, various feedback iteration processes are used in this research. Presented examples and the conducted discussion on the algorithm's operation allow to understand the influence of the proposed modifications on the algorithm's behaviour. Understanding the impact of the proposed modification on the algorithm's operation can be helpful in using it in other algorithms. The obtained images also have potential artistic applications.
|
 |
Gdawiec, K., Shahid, A.A., Nazeer, W.
Mediterranean Journal of Mathematics 17(2), Article number 43, (2020)
Abstract. There are many methods for solving a polynomial equation and many different modifications of those methods have been proposed in the literature. One of such modifications is the use of various iteration processes taken from the fixed point theory. In this paper, we propose a modification of the iteration processes used in the Basic Family of iterations by replacing the convex combination with an s-convex one. In our study we concentrate only on the S-iteration with s-convexity. We present some graphical examples, the so-called polynomiographs, and numerical experiments showing the dependency of polynomiograph's generation time on the value of the s parameter in the s-convex combination.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Symmetry 11(9), 1143, (2019)
Abstract. The aim of this paper is to investigate experimentally and to present visually the dynamics of the processes in which in the standard Newton's root finding method the classic derivative is replaced by the fractional Riemann-Liouville or Caputo derivatives. These processes applied to polynomials on the complex plane produce images showing basins of attractions for polynomial zeros or images representing the number of iterations required to obtain polynomial roots. These latter images were called by Kalantari as polynomiographs. We use both: the colouring by roots to present basins of attractions, and the colouring by iterations that reveal the speed of convergence and dynamic properties of processes visualised by polynomiographs.
|
 |
Wang, X., Yu, T., Chung, K., Gdawiec, K., Ouyang, P.
Symmetry 11(3), 391, (2019)
Abstract. Regular polytopes (RPs) are an extension of 2D (two-dimensional) regular polygons and 3D regular polyhedra in n-dimensional (n ≥ 4) space. The high abstraction and perfect symmetry are their most prominent features. The traditional projections only show vertex and edge information. Although such projections can preserve the highest degree of symmetry of the RPs, they can not transmit their metric or topological information. Based on the generalized stereographic projection, this paper establishes visualization methods for 5D RPs, which can preserve symmetries and convey general metric and topological data. It is a general strategy that can be extended to visualize n-dimensional RPs (n > 5).
|
 |
Bisheh-Niasar, M., Gdawiec, K.
Mathematics and Computers in Simulation 160, 1-12, (2019)
Abstract. In recent years many researchers have focused their attention on the use of different iteration process - known from fixed point theory - in the generation of different kinds of patterns. In this paper, we propose modifications of the Saadatmandi and Bisheh-Niasar root finding method. In the first modification we modify the formula of the method and in the second modification we use the S-iteration with periodic parameters. Moreover, we numerically investigate some properties of the proposed methods and modification using three measures, i.e., the generation time, mean number of iterations and convergence area index. The obtained polynomiographs show that the proposed methods have a potential artistic applications, and the numerical results show that there is no obvious dependency of the considered measures on the sequences of the parameters used in the S-iteration.
|
 |
Kwun, Y.C., Tanveer, M., Nazeer, W., Gdawiec, K., Kang, S.M.
IEEE Access 7, 12167-12176, (2019)
Abstract. Today fractals play an important role in many fields, e.g., image compression or encryption, biology, physics etc. One of the earliest studied fractal types was the Mandelbrot and Julia sets. These fractals have been generalized in many different ways. One of such generalizations is the use of various iteration processes from fixed point theory. In this paper, we study the use of Jungck-CR iteration process extended further by the use of s-convex combination. The Jungck-CR iteration process with s-convexity is implicit three step feedback iteration process. We prove new escape criteria for the generation of Mandelbrot and Julia sets via the proposed iteration process. Moreover, we present some graphical examples obtained by the use of escape time algorithm and the derived criteria.
|
 |
Gościniak, I., Gdawiec, K.
Communications in Nonlinear Science and Numerical Simulation 67, 76-99, (2019)
Abstract. Many algorithms that iteratively find solution of an equation are described in the literature. In this article we propose an algorithm that is based on the Newton-Raphson root finding method and which uses an adaptation mechanics. The adaptation mechanics is based on a linear combination of some membership functions and allows a better control of algorithm's dynamics. The proposed approach allows to visualize the adaptation mechanics impact on the operation of the algorithm. Moreover, various iteration processes and their operation mechanics are discussed in this research. The understanding of the impact of the proposed modifications on the algorithm's operation can be helpful at using other algorithms. The obtained visualizations have also an artistic potential and can be used for instance in creating mosaics, wallpapers etc.
|
 |
Gościniak, I., Gdawiec, K.
Lecture Notes in Computer Science, vol. 11241, pp. 47-56, (2018)
Abstract. In artistic pattern generation one can find many different approaches to the generation process. One of such approaches is the use of root finding methods. In this paper, we present a new method of generating artistic patterns with the use of root finding. We modify the classical Newton's method using a Particle Swarm Optimization approach. Moreover, we introduce various iteration processes instead of the standard Picard iteration used in the Newton's method. Presented examples show that using the proposed method we are able to obtain very interesting and diverse patterns that could have an artistic application, e.g., in texture generation, tapestry or textile design etc.
|
 |
Gdawiec, K., Shahid, A.A.
Open Journal of Mathematical Sciences 2(1), 56-72, (2018)
Abstract. Since the introduction of complex fractals by Mandelbrot they gained much attention by the researchers. One of the most studied complex fractals are Mandelbrot and Julia sets. In the literature one can find many generalizations of those sets. One of such generalizations is the use of the results from fixed point theory. In this paper we introduce in the generation process of Mandelbrot and Julia sets a combination of the S-iteration, known from the fixed point theory, and the s-convex combination. We derive the escape criteria needed in the generation process of those fractals and present some graphical examples.
|
 |
Gdawiec, K.
International Journal of Applied Mathematics and Computer Science 27(4), 827-837, (2017)
Abstract. Aesthetic patterns are widely used nowadays, e.g. in jewellery design, carpet design, as textures and patterns on wallpapers etc. Most of the work during the design stage is carried out by a designer manually. Therefore, it is highly useful to develop methods for aesthetic pattern generation. In this paper, we present methods for generating aesthetic patterns using the dynamics of a discrete dynamical system. The presented methods are based on the use of different iteration processes from fixed point theory (Mann, S, Noor etc.) and the use of an affine combination of these iterations. Moreover, we propose new convergence tests that enrich the obtained patterns. The proposed methods generate patterns in a procedural way and can be easily implemented on the GPU. The presented examples show that using the proposed methods we are able to obtain a variety of interesting patterns. Moreover, the numerical examples show that the use of the GPU implementation using shaders allows the generation of patterns in real time and the speed-up - compared to the CPU implementation - ranges from about 1000 to 2500 times.
|
 |
Gdawiec, K.
Nonlinear Dynamics 90(4), 2457-2479, (2017)
Abstract. Fractal patterns generated in the complex plane by root finding methods are well known in the literature. In the generation methods of these fractals only one root finding method is used. In this paper, we propose the use of a combination of root finding methods in the generation of fractal patterns. We use three approaches to combine the methods: (1) the use of different combinations, e.g. affine and s-convex combination, (2) the use of iteration processes from fixed point theory, (3) multistep polynomiography. All the proposed approaches allow us to obtain new and diverse fractal patterns that can be used, for instance, as textile or ceramics patterns. Moreover, we study the proposed methods using five different measures: average number of iterations, convergence area index, generation time, fractal dimension and Wada measure. The computational experiments show that the dependence of the measures on the parameters used in the methods is in most cases a non-trivial, complex and non-monotonic function.
|
 |
Gdawiec, K., Kotarski, W.
Applied Mathematics and Computation 307, 17-30, (2017)
Abstract. In this paper, an iteration process, referred to in short as MMP, will be considered. This iteration is related to finding the maximum modulus of a complex polynomial over a unit disc on the complex plane creating intriguing images. Kalantari calls these images polynomiographs independently from whether they are generated by the root finding or maximum modulus finding process applied to any polynomial. We show that the images can be easily modified using different MMP methods (pseudo-Newton, MMP-Householder, methods from the MMP-Basic, MMP-Parametric Basic or MMP-Euler-Schroder Families of Iterations) with various kinds of non-standard iterations. Such images are interesting from three points of views: scientific, educational and artistic. We present the results of experiments showing automatically generated non-trivial images obtained for different modifications of root finding MMP-methods. The colouring by iteration reveals the dynamic behaviour of the used root finding process and its speed of convergence. The results of the present paper extend Kalantari's recent results in finding the maximum modulus of a complex polynomial based on Newton's process with the Picard iteration to other MMP-processes with various non-standard iterations.
|
 |
Gdawiec, K.
Computer Graphics Forum 36(1), 35-45, (2017)
Abstract. In this paper, we generalize the idea of star-shaped set inversion fractals using iterations known from fixed point theory. We also extend the iterations from real parameters to so-called q-system numbers and proposed the use of switching processes. All the proposed generalizations allowed us to obtain new and diverse fractal patterns that can be used, e.g., as textile and ceramics patterns. Moreover, we show that in the chaos game for iterated function systems - which is similar to the inversion fractals generation algorithm - the proposed generalizations do not give interesting results.
|
 |
Gdawiec, K.
Nonlinear Dynamics 87(4), 2235-2249, (2017)
Abstract. Mandelbrot and Julia sets are examples of fractal patterns generated in the complex plane. In the literature we can find many generalizations of those sets. One of such generalizations is the use of switching process. In this paper we introduce some switching processes to another type of complex fractals, namely polynomiographs. Polynomiograph is an image presenting the visualization of the complex polynomial's root finding process. The proposed switching processes will be divided into four groups, i.e., switching of: the root finding methods, the iterations, the polynomials and the convergence tests. All the proposed switching processes change the dynamics of the root finding process and allowed us to obtain new and diverse fractal patterns.
|
 |
Gdawiec, K.
Lecture Notes in Computer Science, vol. 9972, pp. 29-36, (2016)
Abstract. In this paper, we present some modifications of inversion fractals. The first modification is based on the use of different metrics in the inversion transformation. Moreover, we propose a switching process between different metric spaces. All the proposed modifications allowed us to obtain new and diverse fractal patterns that differ from the original inversion fractals.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
WSCG 2016 Short Papers Proceedings, pp. 1-5, (2016)
Abstract. In this paper we propose to replace the standard Picard iteration in the Newton--Raphson method by Mann and Ishikawa iterations. This iteration's replacement influence the solution finding process that can be visualized as polynomiographs for the square systems of equations. Polynomiographs presented in the paper, in some sense, are generalization of Kalantari's polynomiography from a single polynomial equation to the square systems of equations. They are coloured based on two colouring methods: basins of attractions with different colours for every real root and colouring dependent on the number of iterations. Possible application of the presented method can be addressed to computer graphics where aesthetic patterns can be used in e.g. texture generation, animations, tapestry design.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Journal of Nonlinear Sciences and Applications 9(5), 2305-2315, (2016)
Abstract. The aim of this paper is to present some modifications of the biomorphs generation algorithm introduced by Pickover in 1986. A biomorph stands for biological morphologies. It is obtained by a modified Julia set generation algorithm. The biomorph algorithm can be used in the creation of diverse and complicated forms resembling invertebrate organisms. In this paper the modifications of the biomorph algorithm in two directions are proposed. The first one uses different types of iterations (Picard, Mann, Ishikawa). The second one uses a sequence of parameters instead of one fixed parameter used in the original biomorph algorithm. Biomorphs generated by the modified algorithm are essentially different in comparison to those obtained by the standard biomorph algorithm, i.e., the algorithm with Picard iteration and one fixed constant.
|
 |
Gdawiec, K.
Advances in Intelligent Systems and Computing, vol. 391, pp. 499-506, (2015)
Abstract. In the paper, a modification of rendering algorithm of polynomiograph is presented. Polynomiography is a method of visualization of complex polynomial root finding process and it has applications among other things in aesthetic pattern generation. The proposed modification is based on a perturbation mapping, which is added in the iteration process of the root finding method. The use of the perturbation mapping alters the shape of the polynomiograph, obtaining in this way new and diverse patterns. The results from the paper can further enrich the functionality of the existing polynomiography software.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Abstract and Applied Analysis, vol. 2015, Article ID 797594, 19 pages, (2015)
Abstract. In this paper a survey of some modifications based on the classic Newton's and the higher order Newton-like root finding methods for complex polynomials are presented. Instead of the standard Picard's iteration several different iteration processes, described in the literature, that we call as non-standard ones, are used. Kalantari's visualizations of root finding process are interesting from at least three points of view: scientific, educational, and artistic. By combining different kinds of iterations, different convergence tests, and different colouring we obtain a great variety of polynomiographs. We also check experimentally that using complex parameters instead of real ones in multi-parameter iterations do not destabilize the iteration process. Moreover, we obtain nicely looking polynomiographs that are interesting from the artistic point of view. Real parts of the parameters alter symmetry, whereas imaginary ones cause asymmetric twisting of polynomiographs.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Wielomianografia z niestandardową rodziną iteracji Eulera-Schrodera
Systemy Inteligencji Obliczeniowej. Uniwersytet Śląski, Katowice, pp. 75-85, (2014)
Streszczenie. Wielomianografia, wprowadzona przez Kalantariego, jest to wizualizacja procesu rozwiązywania równań wielomianowych na płaszczyźnie zespolonej. Łączy w sobie dwa aspekty, matematyczny czyli rozwiązywanie równań z graficzną prezentacją tzw. wielomianografów. Z punktu widzenia grafiki komputerowej ten drugi aspekt wielomianografii jest ważniejszy, gdyż prowadzi do możliwości automatycznego generowania wzorów o walorach estetycznych. Celem pracy jest uogólnienie wielomianografii Kalantariego przez zastosowanie nowych wieloparametrowych schematów iteracyjnych w połączeniu z metodami wyższych rzędów z Rodziny Iteracji Eulera-Schrodera. Wielomianografy otrzymane w ten sposób istotnie poszerzają zbiór możliwych do wygenerowania stabilnych wzorów, które są znacząco różne od motywów generowanych za pomocą standardowej wielomianografii Kalantariego.
|
 |
Gdawiec, K.
Fractals 22(4), 1450009, 7 pages, (2014)
Abstract. In the paper, we generalized the idea of circle inversion to star-shaped sets and used the generalized inversion to replace the circle inversion transformation in the algorithm for the generation of the circle inversion fractals. In this way, we obtained the star-shaped set inversion fractals. The examples that we have presented show that we were able to obtain very diverse fractal patterns by using the proposed extension and that these patterns are different from those obtained with the circle inversion method. Moreover, because circles are star-shaped sets, the proposed generalization allows us to deform the circle inversion fractals in a very easy and intuitive way.
|
 |
Gdawiec, K.
Lecture Notes in Computer Science, vol. 8671, pp. 25-32, (2014)
Abstract. Polynomiography is a method of visualization of complex polynomial root finding process. One of the applications of polynomiography is generation of aesthetic patterns. In this paper, we present two new algorithms for polynomiograph rendering that allow to obtain new diverse patterns. The algorithms are based on the ideas used to render the well known Mandelbrot and Julia sets. The results obtained with the proposed algorithms can enrich the functionality of the existing polynomiography software.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
WSCG 2014 Poster Papers Proceedings, pp. 21-26, (2014)
Abstract. In the paper visualizations of some modifications based on the Newton's root finding of complex polynomials are presented. Instead of the standard Picard iteration several different iterative processes described in the literature, that we call as non-standard ones, are used. Following Kalantari such visualizations are called polynomiographs. Polynomiographs are interesting from scientific, educational and artistic points of view. By the usage of different kinds of iterations we obtain quite new, comparing to the standard Picard iteration, polynomiographs that look aesthetically pleasing. As examples we present some polynomiographs for complex polynomial equation z^3 - 1 = 0. Polynomiographs graphically present dynamical behaviour of different iterative processes. But we are not interested in it. We are focused on polynomiographs from the artistic point of view. We believe that the new polynomiographs can be interesting as a source of aesthetic patterns created automatically. They also can be used to increase functionality of the existing polynomiography software.
|
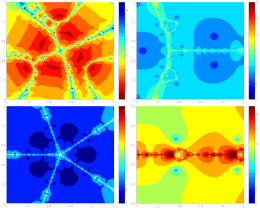 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Wielomianografia wyższych rzędów z iteracjami Manna i Ishikawy
Systemy Wspomagania Decyzji. Uniwersytet Śląski, Katowice, pp. 171-181, (2013)
Streszczenie. Celem tego rozdziału jest przedstawienie modyfikacji wielomianografii wyższych rzędów uzyskanej poprzez zastąpienie standardowej iteracji Piccarda przez iterację Manna i Ishikawy. Wielomianografia, odkryta przez Kalantariego w 2000 roku, jest to wizualizacja procesu aproksymacji miejsc zerowych wielomianu zespolonego. Wielomianografia wiąże matematykę ze sztuką. Jest metodą, za pomocą której generuje się wzory o dużych walorach estetycznych. Zaproponowana w rozdziale modyfikacja wielomianografii prowadzi do istotnego poszerzenia zbioru możliwych do wygenerowania wzorów, które mogą być inspiracją dla grafików. Może ponadto rozszerzyć możliwości istniejącego oprogramowania do generowania wielomianografów.
|
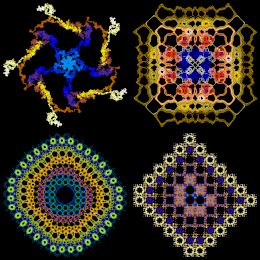 |
Gdawiec, K.
Lecture Notes in Computer Science, vol. 8104, pp. 358-366, (2013)
Abstract. The aim of this paper is to present some modifications of the orbits generation algorithm of discrete dynamical systems. The first modification is based on introduction of a perturbation mapping in the standard Picard iteration used in the orbit generation algorithm. The perturbation mapping is used to alter the orbit during the iteration process. The second modification combines the standard Picard iteration with the iteration which uses the perturbation mapping. The obtained patterns have unrepeatable structure and aesthetic value. They can be used for instance as textile patterns, ceramics patters or can be used in jewellery design.
|
 |
Gdawiec, K.
WSCG 2013 Communication Proceedings, pp. 15-20, (2013)
Abstract. The aim of this paper is to present a modification of the visualization process of finding the roots of a given complex polynomial which is called polynomiography. The name polynomiography was introduced by Kalantari. The polynomiographs are very interesting both from educational and artistic points of view. In this paper we are interested in the artistic values of the polynomiography. The proposed modification is based on the change of the usual convergence test used in the polynomiography, i.e. using the modulus of a difference between two successive elements obtained in an iteration process, with the tests based on distance and non-distance conditions. Presented examples show that using various convergence tests we are able to obtain very interesting and diverse patterns. We believe that the results of this paper can enrich the functionality of the existing polynomiography software.
|
 |
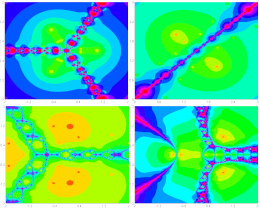
Kotarski, W., Gdawiec, K., Lisowska, A.
Metody generowania estetycznych wzorów
Systemy Wspomagania Decyzji. Uniwersytet Śląski, Katowice, pp. 331-339, (2012)
Streszczenie. W pracy przedstawiono wybrane metody generowania estetycznych wzorów za pomocą komputera. Do prezentacji wybrano trzy metody oparte na różnych podejściach: systemach dynamicznych, biomorfach oraz wielomianografii, które generują szerokie spektrum wzorów o dużych potencjalnych możliwościach ich praktycznego zastosowania. Wzory generowane automatycznie, na podstawie wybranych metod, mogą stanowić inspirację dla grafików komputerowych. Ponadto, metody te wzbogacone dodatkowo o formalne kryteria oceniające miarę estetyki generowanych wzorów takie jak: złożoność, symetrie, zwartość, spójność, wymiar fraktalny, mogą tworzyć podstawę systemu generującego automatycznie wzory o zadanych przez użytkownika parametrach estetycznych.
|
 |
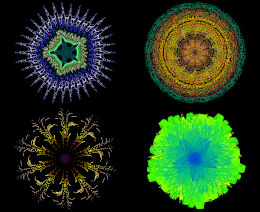
Kotarski, W., Gdawiec, K., Lisowska, A.
Lecture Notes in Computer Science, vol. 7431, pp. 305-313, (2012)
Abstract. The aim of this paper is to present some modifications of complex polynomial roots finding visualization process. In this paper Ishikawa or Mann iterations are used instead of the standard Picard iteration. Kalantari introduced the name polynomiography for that visualization process and the obtained images he called polynomiographs. Polynomiographs are interesting both from educational and artistic point of view. By the use of different iterations we obtain quite new polynomiographs that look aestheatically pleasing comparing to the ones from standard Picard iteration. As examples we present some polynomiographs for complex polynomial equation z^3 - 1 = 0, permutation and doubly stochastic matrices. We believe that the results of this paper can inspire those who may be interested in aesthetic patterns created automatically. They also can be used to increase functionality of the existing polynomiography software.
|
Gdawiec, K., Domańska, D.
Lecture Notes in Artificial Intelligence, vol. 7267, pp. 501-508, (2012)
Abstract. The aim of this paper is to present a new method of two-dimensional shape recognition. The method is based on dependence vectors which are fractal features extracted from the partitioned iterated function system. The dependence vectors show the dependency between range blocks used in the fractal compression. The effectiveness of our method is shown on four test databases. The first database was created by the authors and the other ones are: MPEG7 CE-Shape-1PartB, Kimia-99, Kimia-216. Obtained results have shown that the proposed method is better than the other fractal recognition methods of two-dimensional shapes.
|
|
Gdawiec, K., Domańska, D.
International Journal of Applied Mathematics and Computer Science 21(4), 757-767, (2011)
Abstract. One of the approaches in pattern recognition is the use of fractal geometry. The property of self-similarity of fractals has been used as a feature in several pattern recognition methods. All fractal recognition methods use global analysis of the shape. In this paper we present some drawbacks of these methods and propose fractal local analysis using partitioned iterated function systems with division. Moreover, we introduce a new fractal recognition method based on a dependence graph obtained from the partitioned iterated function system. The proposed method uses local analysis of the shape, which improves the recognition rate. The effectiveness of our method is shown on two test databases. The first one was created by the authors and the second one is the MPEG7 CE-Shape-1 PartB database. The obtained results show that the proposed methodology has led to a significant improvement in the recognition rate.
|
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Automatyczne generowanie estetycznych wzorów za pomocą transformacji Gumowskiego-Miry
Systemy Wspomagania Decyzji. Uniwersytet Śląski, Katowice, pp. 219-226, (2011)
Streszczenie. Celem niniejszej pracy jest przedstawienie sposobu użycia jednego z dyskretnych układów dynamicznych, tj. transformacji Gumowskiego-Miry, do automatycznego generowania estetycznych wzorów. Zaprezentowane zostaną również trzy algorytmy kolorowania otrzymanych wzorów. Przedstawione przykłady pokazują ogromne możliwości tworzenia niepowtarzalnych wzorów za pomocą zaprezentowanych algorytmów. Wygenerowane za pomocą zaproponowanego algorytmu wzory mogą zostać użyte jako wzory na tkaniny, ceramikę czy też jako podstawa do wykonania różnego rodzaju ozdób czy biżuterii.
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Lecture Notes in Computer Science, vol. 6939, pp. 691-700, (2011)
Abstract. The aim of this paper is to present some modifications of the orbits generation algorithm of dynamical systems. The well-known Picard iteration is replaced by the more general one - Krasnosielskij iteration. Instead of one dynamical system, a set of them may be used. The orbits produced during the iteration process can be modified with the help of a probabilistic factor. By the use of aesthetic orbits generation of dynamical systems one can obtain unrepeatable collections of nicely looking patterns. Their geometry can be enriched by the use of the three colouring methods. The results of the paper can inspire graphic designers who may be interested in subtle aesthetic patterns created automatically. |
 |
Kotarski, W., Gdawiec, K., Lisowska, A.
Nieliniowe podziały i fraktale
Systemy Wspomagania Decyzji. Uniwersytet Śląski, Katowice, pp. 363-371, (2010)
Streszczenie. W pracy przedstawia się uogólnienia techniki podziałów, których zastosowanie prowadzi do możliwości wygenerowania gładkich obiektów graficznych takich jak krzywe, płaty czy obiektów fraktalnych na podstawie początkowego zbioru punktów. Uogólnienia te idą w dwóch kierunkach. Pierwszy wprowadza parametr zespolony do podziału liniowego, zaś drugi nieliniowość za pomocą średnich innych niż średnia arytmetyczna. Omawiane uogólnienia podziałów w sposób istotny rozszerzają klasę obiektów graficznych, którą można wygenerować za pomocą liniowych podziałów. Podziały pozostają w ścisłym związku z metodami fraktalnymi, gdyż za ich pomocą i zadanego zbioru punktów kontrolnych definiuje się układy IFS stosowane do fraktalnego renderingu obiektów graficznych. W pracy jest również przedstawiony związek między podziałami i fraktalami. Wskazano ponadto na pewne zastosowania metody podziałów.
|
 |
Kotarski, W., Gdawiec, K., Lisowska, A.
On Gumowski-Mira Aesthetic Superfractal Forms
Proceedings of The 2010 IRAST International Congress on Computer Applications and Computational Science, pp. 562-565, (2010)
Abstract. Gumowski-Mira transform, in short GM, produces nice looking fractal forms that can be used to model ,,marine living creatures'' or aesthetic patterns useful for artistic design. Those original unrepeatable forms can inspire artistic design in jewellery such as pendants, necklaces, talismans. Moreover, GM can be a source of texture patterns for computer graphics and it suggests motives for fractal arts. We show that combination of GM with superfractals lead to enlarging a variety of fractal forms possible to create. Colours added to geometry enrich aesthetic appearance of superfractal forms generated with the help of GM.
|
Gdawiec, K.
Lecture Notes in Artficial Intelligence, vol. 6401, pp. 403-410, (2010)
Abstract. From the beginning of fractal discovery they found a great number of applications. One of those applications is fractal recognition. In this paper we present some of the weaknesses of the fractal recognition methods and how to eliminate them using the pseudofractal approach. Moreover we introduce a new recognition method of 2D shapes which uses fractal dependence graph introduced by Domaszewicz and Vaishampayan in 1995. The effectiveness of our approach is shown on two test databases.
|
|
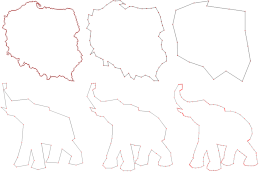 |
Kotarski, W., Gdawiec, K.
Proste i odwrotne schematy podziału
Systemy Wspomagania Decyzji. Uniwersytet Śląski, Katowice, pp. 229-238, (2009)
|
 |
Gdawiec, K., Kotarski, W., Lisowska, A.
Fractal Rendering of Arbitrary Catmull-Clark Surfaces
Computer Methods and Systems 2009, Kraków, pp. 401-406
Abstract. In the paper we deal with the fractal rendering of arbitrary Catmull-Clark surfaces. To obtain Iterated Function System (IFS) needed for surface generation we use some facts about approximation of Catmull-Clark surface and fractal description of bicubic patches. First we approximate the given Catmull-Clark surface with bicubic B\'ezier patches and then for each patch we find corresponding IFS. In this way we obtain fractal description of the surface and therefore we can generate it fractally. Further, some examples of Catmull-Clark surfaces rendered fractally are also presented.
|
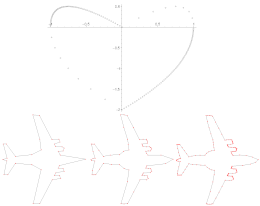 |
Kotarski, W., Gdawiec, K., Machnik, G.T.
Fractal Based Progressive Representation of 2D Contours
Computer Methods and Systems 2009, Kraków, pp. 407-412
Abstract. In the paper we present a method, different from those presented in literature, for progressive representation of two dimensional contours. The method is based on fractal representation of a set of linear and quadratic curves that approximate a given contour. If one knows IFS for fractal rendering of every part of the contour, then using the set of all IFSs (the so-called PIFS) it is possible to generate that contour fractally. When starting iterations from a single points belonging to the segments of the contour in every iteration further points lying on the contour are generated. In every iteration number of points placed on the contour is doubling. So, the contour is presented progressively in higher and higher resolution showing gradually larger number of details.
|
Gdawiec, K.
Advances in Intelligent and Soft Computing, vol. 59, pp. 451-458, (2009)
Abstract. One of approaches in pattern recognition is the use of fractal geometry. The property of the self-similarity of the fractals has been used as feature in several pattern recognition methods. In this paper we present a new fractal recognition method which we will use in recognition of 2D shapes. As fractal features we used Partitioned Iterated Function System (PIFS). From the PIFS code we extract mappings vectors and numbers of domain transformations used in fractal image compression. These vectors and numbers are later used as features in the recognition procedure using a normalized similarity measure. The effectiveness of our method is shown on two test databases. The first database was created by the author and the second one is MPEG7 CE-Shape-1PartB database.
|
|
Gdawiec, K.J.
IEEE Eurocon 2009, St. Petersburg, Russia, pp. 353-358
Abstract. From the beginning of fractals discovery they found a great number of applications. One of those applications is fractal recognition. In this paper we introduce a fractal recognition method which is based on fractal description obtained from fractal image compression. Next, we present simple modification of this method and results of the tests.
|
|
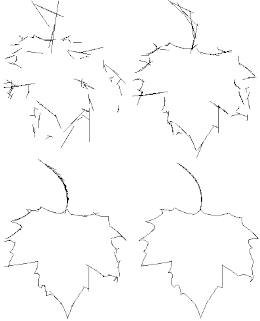 |
Gdawiec, K.
International Journal of Pure and Applied Mathematics 50(3), 421-430, (2009)
Abstract. The problem of fractal modeling is very simple when we know the mathematical description of a fractal. We just apply one of the well-known algorithms. The inverse problem of finding the mathematical description for given fractal is not so trivial and we do not know any general method to solve this problem. So there are several approaches to this problem e.g. via Bezier curves, fractal compression. In this paper we present automatic method for finding fractal description of 2D contours. Our algorithm uses fractal interpolation for this purpose. We also present some of practical examples.
|
Gdawiec, K., Kotarski, W.
Fraktalne rozpoznawanie obiektów dwuwymiarowych
Systemy Wspomagania Decyzji. Uniwersytet Śląski, Katowice, pp. 261-268 (2008)
Streszczenie. Od momentu odkrycia fraktale znalazły szerokie zastosowania. Jednym z takich zastosowań jest wykorzystanie ich do rozpoznawania kształtów. W niniejszym artykule przedstawimy dwie metody fraktalnego rozpoznawania oparte o opis fraktalny powstający w wyniku fraktalnej kompresji obrazów. Następnie omówimy prostą modyfikację tych metod oraz wyniki przeprowadzonych badań.
|
Popularnonaukowe
Bała, A., Gdawiec, K.
No Limits 2(8), 18-21, (2023)
|
Inne
 |
Gdawiec, K.
MathWorks, (2006)
|
 |
Gdawiec, K.
MathWorks, (2006)
|

